Specific Strength vs Specific Modulus: Material Selection

Lightweight design depends on whether your component fails by breaking or by bending. This guide explains how to use specific strength and specific modulus correctly in real material selection, including Ashby indices, geometry effects, and verified data comparisons.

Download the Specific Strength vs Specific Modulus PDF

Specific strength and specific modulus are screening ratios for lightweight design.

• Specific strength (σ/ρ) governs strength-limited parts such as ties or tension members.
  
  

• Specific modulus (E/ρ) governs stiffness-limited parts such as beams, panels, and struts.
  Choosing the wrong ratio causes under- or over-designed sections.

Material selection goes wrong when you compare “good-looking” ratios without a load case. A bracket fails, and everyone blames a low grade. In reality, the bracket was stiffness-limited, not strength-limited. The part did not crack first. It bent, opened a gap, shifted the load path, and then a fastener or weld took a peak load it never saw in the spreadsheet.

Two ratios sit at the center of this problem. One relates strength to density. The other relates stiffness to density. Each ratio is valid, but only inside its correct failure story. You also need to respect geometry because beams, plates, and columns do not scale the same way with material properties.

In practice, I treat these ratios as filters, not final answers. A ratio gets you into a shortlist. After that, you check fatigue, temperature, corrosion, joining, and variability. This article builds that full decision chain, so your next design review has fewer opinions and more physics.

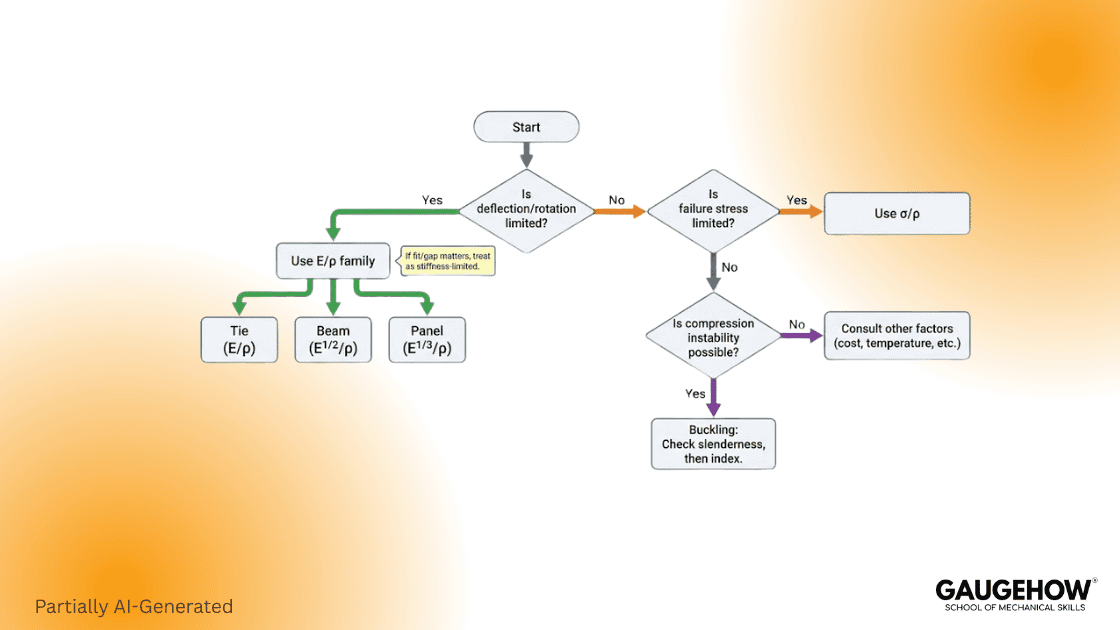
Quick Decision Rule

Use this flow as your decision aid. It keeps you honest when the team starts chasing “lightweight” numbers.

Start

  |

  |-- Is maximum deflection/rotation a hard requirement?

  |        |

  |        |-- YES --> Stiffness-Limited --> Use modulus-to-density style indices

  |        |

  |        |-- NO  --> Go next

  |

  |-- Is the first failure governed by yield/ultimate or buckling?

           |

           |-- Yield/Ultimate --> Strength-Limited --> Use strength-to-density style indices

           |

           |-- Buckling       --> Stiffness + Geometry --> Use stiffness-based buckling indices

One practical shortcut helps. If your drawing has a tight flatness, gap, or alignment tolerance under load, treat it as stiffness-limited. If your drawing has a high proof load and no deflection cap, treat it as strength-limited.

Definitions And Units

• Specific strength = Strength ÷ Density.

It expresses how much load a material can take per unit mass and is measured in N·m/kg or kJ/kg.

Used mainly in strength-limited members like rods, bolts, or cables.

• Specific modulus (specific stiffness) = Young’s modulus ÷ Density.

It expresses stiffness efficiency per unit mass and is used in stiffness-limited structures like beams or panels.

Units reminder

• Modulus in GPa and density in g/cm³ give convenient numeric ratios (GPa·cm³/g).
  
  

• Always keep consistent units; mixed systems lead to false comparisons.

Units And Quick Conversions

People lose time here, so I keep it strict.

Strength divided by density can be written several ways. Using SI base units, Pa divided by kg/m³ becomes N·m/kg, which is J/kg. That is why specific strength is often shown as kJ/kg in handbooks. (Wikipedia)

E divided by density has the same unit structure. It is also a form of energy per unit mass, even though you should treat it as a stiffness efficiency, not stored energy.

Two notes prevent classic review-room mistakes:

• Keep yield and ultimate separate. A metal “strength” line in a datasheet might mean either. (AZoM)

• Always write the source for density. A composite ply, a laminate, and a fiber tow are different materials.

You will see modulus units written as GPa and density as g/cm³ in many tables because the ratio becomes numerically convenient (GPa·cm³/g). (Stanford Advanced Materials)

Those stiffness units are valid as long as you stay consistent across all candidates. (Wikipedia)

Ashby Indices Table

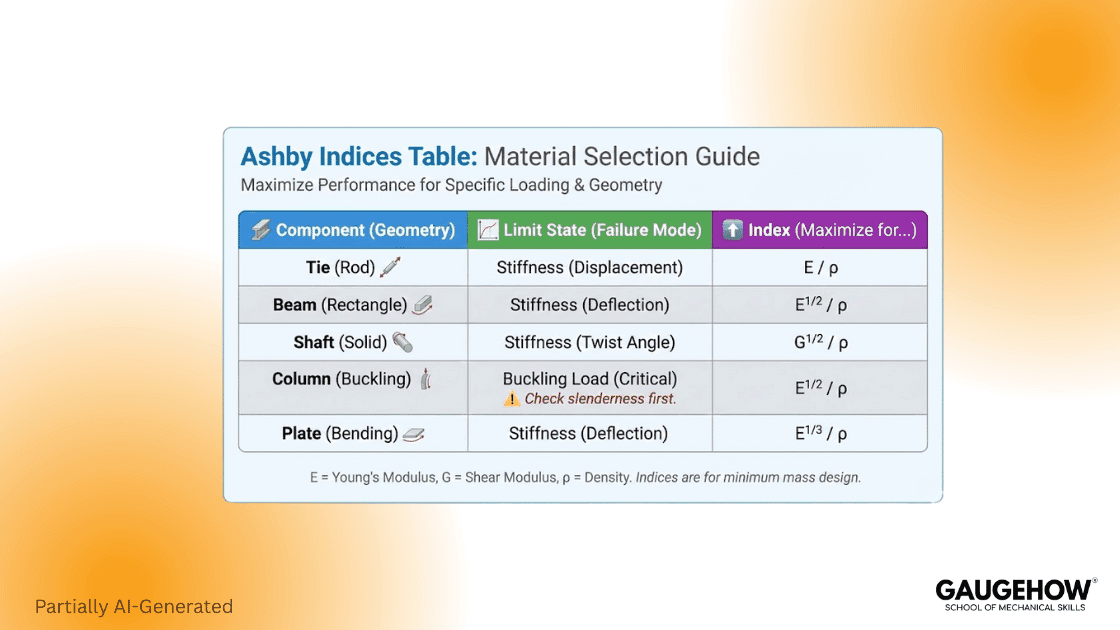
The table below condenses the geometry-complete Ashby approach used in mechanical design selection charts.

How to use it:

1. Define the limit state: breakage or deflection.
   
   

2. Pick the right geometry row.
   
   

3. Use yield strength for ductile metals; ultimate for brittle ones.
   
   

4. Use E when stiffness or vibration governs.
   
   

5. Record index and property sources in reviews.

Geometry Driven Indices

This is the section most “comparison” articles skip, and it is where real weight gets saved.

A ratio is only a full answer for a specific structural form.

Ties And Rods In Tension

If a straight tie carries axial load and you size it by stress, mass scales with strength divided by density. That is the clean home of the classic strength-to-weight ratio.

If the same tie is sized by extension limit, stiffness matters, and E divided by density becomes the driver.

Beams In Bending

Beams are different becausethe second moment of area moves faster than area when you change shape. For stiffness-limited beams, the classic light stiff objective pushes you toward a square root dependence on E rather than a linear dependence. That is why two metals with similar E/ρ can still behave differently after you change the section architecture.

Plates And Panels

Plates under bending stiffness constraints typically use an even weaker exponent on E. In other words, geometry dominates. That is why honeycomb and sandwich panels beat “better metals” in many stiffness-limited problems.

Buckling Members

Columns and thin shells fail by instability long before yield, especially in compression. Any selection that ignores buckling is incomplete. In buckling limited regimes, stiffness and slenderness couple, so you should treat the material ratio as only half the story.

How We Think Differently
A good material is one that survives the real failure mode with the lowest mass. That statement forces you to write the limit state first. Once the limit state is correct, the material chart usually agrees with your intuition.

Verified Numeric Anchor

NPTEL notes report that the specific stiffness of advanced fibers is ~13× higher and the specific strength ~16× higher than that of structural metals. This explains why composites dominate stiffness-limited aerospace and EV shell design. (Source: NPTEL Materials for Engineers)

Decision Traps

Why Steel and Aluminum Feel Similar in Stiffness per kg

Despite popular belief, stiffness per mass differs by only ~4-5%. So in stiffness-limited problems, geometry optimization—depth, ribbing, sandwich panels—beats switching alloys.

When Strength Ratios Mislead

A high σ/ρ looks great until the real failure mode is buckling, bearing, or fatigue. Always identify the limit state before screening.

Buckling Members Need Slenderness First

For columns and shells, the slenderness ratio and end constraints decide the load first. The stiffness index only screens materials after geometry stabilizes.

Material Comparisons

Interpretation:

• Most metals cluster near E/ρ ≈ 25, so stiffness per mass stays flat.
  
  

• Composites jump 4–5× in stiffness per mass and ~16× in strength per mass.
  
  

• If stiffness limits, composites win. If strength limits, titanium or high-Mg alloys excel.

Worked Comparison With Real Materials

Below is a compact, traceable comparison using commonly referenced grades and datasheets.

Input Properties 

• ASTM A36 steel: density 7.85 g/cm³, yield 250 MPa, modulus 200 GPa (AZoM)

• 6061 T6 aluminum: density 2.70 g/cc, yield 276 MPa, modulus 68.9 GPa (gabrian.com)

• Ti 6Al 4V: density 4.43 g/cc, yield (0.2% offset, min) 827 MPa, modulus 114 GPa (maher.com)

• Magnesium AZ31B: density 1.77 g/cm³, yield (0.2% offset) 200 MPa, modulus 44.8 GPa (AZoM)

• Carbon fiber T300 (fiber): density 1.76 g/cm³, tensile strength 3530 MPa, tensile modulus 230 GPa

Computed Ratios (Same Units Across All)

Stiffness efficiency (E/ρ):

• A36: 200 / 7.85 ≈ 25.5

• 6061 T6: 68.9 / 2.70 ≈ 25.5

• Ti 6Al 4V: 114 / 4.43 ≈ 25.7

• AZ31B: 44.8 / 1.77 ≈ 25.3

• T300 fiber: 230 / 1.76 ≈ 131

This result is the punchline many teams need to hear: most common structural metals cluster around the same stiffness per weight. (Stanford Advanced Materials)

If your part is stiffness-limited, changing steel to aluminum often does less than people expect unless you also change section geometry.

Strength efficiency (strength/ρ, using yield for metals):

• A36: 250 / 7.85 ≈ 31.8

• 6061 T6: 276 / 2.70 ≈ 102

• Ti 6Al 4V: 827 / 4.43 ≈ 187

• AZ31B: 200 / 1.77 ≈ 113

• T300 fiber (tensile): 3530 / 1.76 ≈ 2006

Now the pattern flips. Strength per weight varies a lot, especially once you include high-performance alloys and fibers. (AZoM)

What This Means In Design Terms

If your component is strength-limited, titanium can reduce mass even when modulus per weight is not impressive.

If your component is stiffness-limited, a metal swap alone is rarely a breakthrough. In that case, you usually need either a composite, a sandwich concept, or a geometry change that raises bending stiffness faster than mass.

That is also why the specific strength formula belongs in your early screening notes, not at the end. Use it to rule out obvious losers, then move to geometry-specific indices.

Mini Calculator and Download

Inputs

• Strength σ (MPa)
  
  

• Modulus E (GPa)
  
  

• Density ρ (kg/m³ or g/cm³)

Outputs

• Specific Strength = σ / ρ
  
  

• Specific Modulus = E / ρ
  
  

• Beam Index = E^(1/2)/ρ
  
  

• Panel Index = E^(1/3)/ρ

Use it during concept screening, then verify the real limiter (fatigue, temperature, joints).

Download the Specific Strength vs Specific Modulus Index Card

Common Pitfalls And Practical Shortlists

Pitfalls I See In Real Builds

• Confusing material stiffness with part stiffness. A high modulus does not save a poor section design.

• Using ultimate strength where yield governs. That error hides permanent set and assembly stack issues. (AZoM)

• Ignoring compression failure in composites. Tensile strength looks great, but compressive and shear allowables often govern joints and bearing.

• Skipping buckling checks. Thin members fail by instability first in many lightweight programs.

Practical Shortlists By Problem Type

For fast early selection, I use shortlists like this and then validate with real allowables.

If you are stiffness-limited:
Choose metals for cost, corrosion, and joining first, because their stiffness per weight is similar. When you need a step change, look at fiber composites or sandwich constructions. (Stanford Advanced Materials)

If you are strength-limited:
Aluminum and magnesium can beat mild steel in mass, but you must account for fatigue and corrosion. Titanium becomes attractive when corrosion, temperature, or safety factors dominate. (gabrian.com)

Here is the sanity check I enforce in reviews: show one table with load case, limit state, and the chosen index. If that line is missing, the ratio comparison is noise.

Also, remember why searchers keep typing “strength to weight ratio” into Google. They are looking for a shortcut, so give them one, but keep the failure mode honest.

FAQ

1) When should I prioritize specific modulus over strength ratios?

Prioritize it when deflection, vibration, or alignment is the first failure condition. That choice is usually driven by requirements like gap, stiffness, or eigenfrequency limits. (Stanford Advanced Materials)

2) Why do steels and aluminum feel similar in terms ofstiffness per weight?

Because E scales with density across many metals, their E/ρ values cluster in a narrow band. That shows up clearly when you compute it using typical grade data. (gabrian.com)

3) What is the biggest mistake with composites in ratio comparisons?

People use fiber tensile numbers as if the structure is isotropic. Real laminates must be checked in shear, compression, bearing, and with manufacturing variability.

4) How do I report ratios cleanly in a design review?

State the load case, state the limit state, then show the ratio used for screening and the property source. Without that chain, the comparison cannot be audited.

5) Do “units” matter if I only compare materials?

Consistency matters more than the unit label. Keep modulus and density in matched systems, and do not mix supplier and handbook values without noting temperature and temper. (gabrian.com)

References

1. Wikipedia, “Specific strength” (Wikipedia)

2. Wikipedia, “Specific modulus” (Wikipedia)

3. AZoM, ASTM A36 steel properties (density, yield, modulus) (AZoM)

4. Gabrian, 6061 T6 properties (density, yield, modulus) (gabrian.com)

5. Maher, Ti 6Al 4V datasheet (density, yield, modulus) (maher.com)

6. AZoM, Magnesium AZ31B properties (density, yield, modulus) (AZoM)

7. Toray, T300 technical data sheet (density, tensile modulus, tensile strength)

8. University of Cambridge, material selection charts hub (chart approach, specific stiffness vs specific strength chart) (Materials Engineering Cambridge)